Research Topics

研究テーマの詳細
JAXA 宇宙科学研究所での研究　 NASA GLENN RESEARCH CENTERでの研究　東北大学での研究

JAXA宇宙科学研究所での研究テーマ
これらの研究の多くは宇宙研・藤井孝藏教授と一緒に行っています．

次期火星探査ミッションMELOS-1への搭載を目指した小型火星飛行機の空力設計に関する研究(2009-)
現在，2020年の打ち上げを目標とした次期火星探査ミッションMELOS-1が検討されている．このMELOS-1での火星の飛翔探査を目的として，小型火星飛行機の設計検討が行われており，本研究では，小型火星飛行機の空力設計に関する研究を行っている．これまでの研究により火星大気中では地球上ほど翼端抵抗が大きくなく，さほど高アスペクト比な翼でなくとも抵抗が小さくなることなどを明らかにしている．

羽ばたき型火星航空機の空気力学に関する研究(2004-)
近年，次世代の火星探査のアプローチの一つとして，羽ばたき型の航空機による探査が注目されている．火星航空機は少ない消費エネルギーで大きな揚力と推力を発生させなければならないが，これまで行われてきた羽ばたきに関する研究は推力のみ，もしくは推進効率のみに注目した研究がほとんどである．本研究では数値流体力学と数値最適化手法，自己組織化マップ等を用いてエネルギー消費を小さく抑えつつ揚力と推力双方を大きくする羽ばたき方について研究を行っている．

再使用観測ロケットの空力設計最適化に関する研究(2008-)
宇宙航空研究開発機構で研究開発が進められている高度100km以上まで上昇可能な再使用観測ロケットの空力設計最適化に関する研究を稲谷研究室と共同で２００８年度から行っています．２００９年度は機体の空力設計の多目的最適化・多目的設計探査を行いました．今後もこの研究は続けたいと思っています．

宇宙機の軌道の多目的設計探査(2009-)
2009年度から，宇宙研・川勝准教授と次期太陽観測衛星SOLAR-Cの機体・軌道の多目的設計探査に取り組み始めました．多目的設計探査手法を用いることで複数の目的関数のトレードオフ情報や設計変数の感度情報などが明らかにされつつあります

パレート最適解からの知識抽出法についての研究(2007-)
多目的設計最適化問題の最適解をパレート最適解といいます．このパレート最適解から設計者にとって有益な情報を引き出すことはとても重要ですが，この点に関してはまだ研究が十分にはなされていません．本研究ではパレート最適解からの知識抽出方法について研究を行っています．

DBDプラズマアクチュエータによる流れ制御に関する研究(2006-)
DBDプラズマアクチュエータという流れ制御デバイスを用いた翼周りの流れの制御に関する研究を２００６年度から開始しています．今年度は超音速キャビティ流れの制御にも取り組んでいます．
　　　

ハイブリッドロケットの概念設計の多目的設計探査(2008-2010)
ハイブリッドロケットは運用コストが小さい，安全性が高い，スロットリングが可能であるなどの利点を持つ次世代ロケットの候補の１つである．本研究では，バイブリッドロケットの概念設計評価プログラムを開発し，多目的設計探査プログラムと組み合わせることで，ハイブリッドロケット概念設計の多目的設計探査を行いました．この研究は現在は首都大学東京の金崎雅博准教授に引き継いでもらっています．

ロケットエンジン用ターボポンプの設計最適化に関する研究(2007-)
JAXAで研究が進められている次世代ロケットエンジン(LE-X)のターボポンプの設計最適化に関する研究をJAXA情報・計算工学センターと共同で行っています．

丸い前縁を持つデルタ翼流れにおける一様流マッハ数効果に関する実験的研究(2006- 2008)
宇宙科学研究本部の遷・超音速風洞を用いて，丸い前縁を持つデルタ翼周りの流れに与える一様流マッハ数及び迎角の効果に関する研究を行った．マッハ数が 0.7～の条件について，デルタ翼上面流れに与える影響を感圧塗料とオイルフローを用いて調べることで，遷・超音速領域でコード方向に２種類の流れ場構造が混在する遷移流れ場が存在することを明らかにした．また，遷移流れ場の境界の位置がマッハ数および迎角によって変化することを明らかにした．

基幹ロケットバルブの設計開発プロセス情報化による基幹ロケットの高信頼性化(2003- 2008)
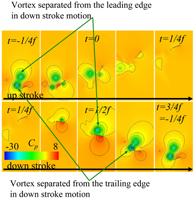
基幹ロケットバルブの信頼性を向上させるため，バルブ設計開発プロセスの高信頼性化に取り組んでいる．これまで発生した不具合と類似の不具合を今後発生させないことを目的に詳細FMEA，FTAおよびQFDの利用方法についての検討を行い，詳細FMEAからFTAへの自動変換手法などを考案し，ソフトウェアを開発している．

再使用観測ロケットの空力特性に関する数値力学研究(2005-2007)
宇宙科学研究本部で進められている再使用観測ロケットシステムでは，必要なダウンレンジを得るために機体にノーズエントリ・テールランディング方式を採用する計画であり，着陸前に機体を反転させることが必要となる．このような機体運動はこれまでのロケットにないものであり，機体反転時の空力特性の把握と関連する機体周りの流れ場の理解が必要である．本研究では実機の反転時に考えられる迎角について，数値流体力学を用いてパラメトリックスタディを行い，それぞれの迎角におけるピッチングモーメント係数などの空力係数と流れ場構造について考察を行った．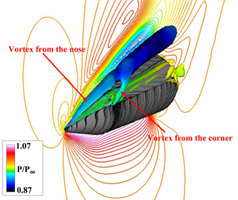

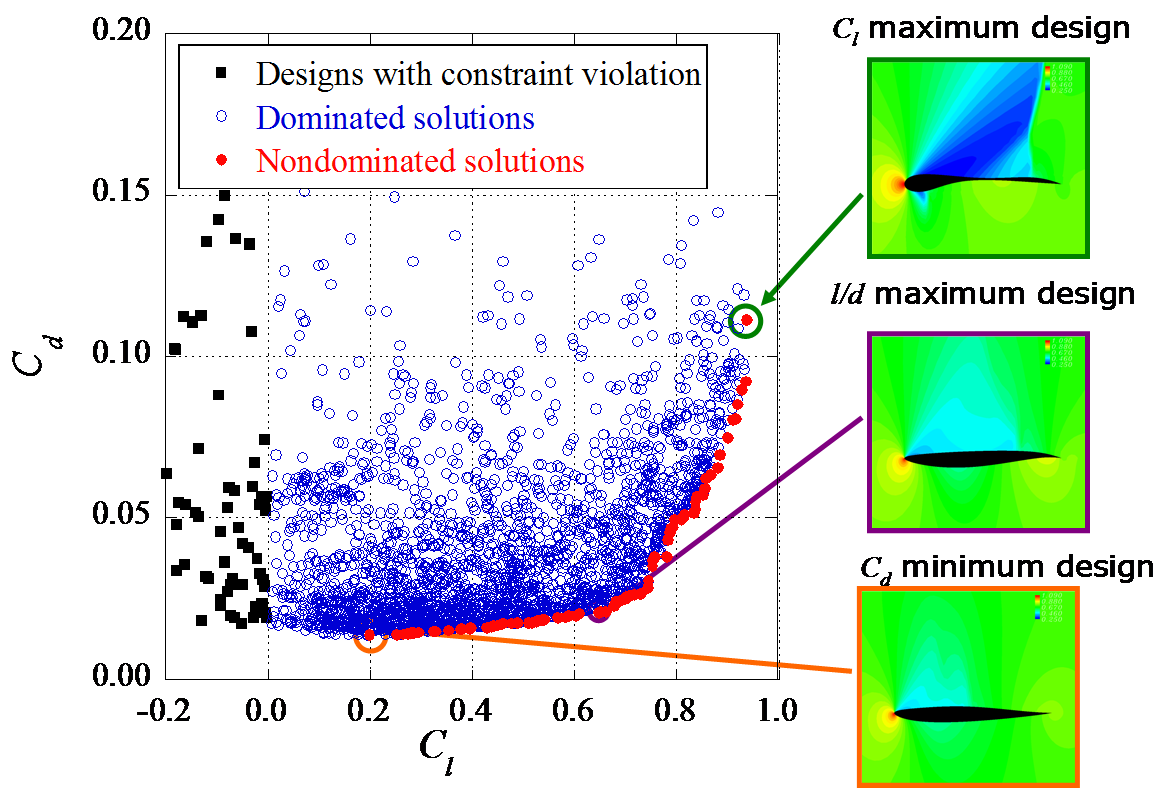
惑星飛行機用低レイノルズ数翼型の空力最適化に関する研究(2004-2006)
これまでの火星表面での探査はローバーに限定されているが，行動範囲が限られるという欠点を持つため，より広い領域を探査が可能な航空機型の火星探査機が注目されている．しかしながら，火星の大気環境は地球と大きく異なるため，マッハ数・レイノルズ数が地球上の一般的な航空機の飛行条件とは大きく異なると考えられる．そのため，火星航空機には地球上で使われている飛行機の翼型とはちがうまったく新しい翼型が必要となる可能性がある．本年度は，いくつかのマッハ数条件，レイノルズ数条件において進化的計算法と数値流体力学を用いて空気力学的に最適な翼型形状を求め，マッハ数およびレイノルズ数が最適翼型形状に与える影響についての知見を明らかにした．

高効率かつ利便性に優れた新たなロバスト最適化手法の開発(2003-2006)
実際の工学設計では，設計，製造の過程で誤差等の不確定性や実際の運用条件の変動が含まれるため，単純に性能向上だけを目的とする従来の最適化計算では期待される性能が実現されないことがある．そこで近年，不確定性を考慮した設計最適化技術として，ロバスト最適化が注目を浴びている．本研究では，既存手法である「シックスシグマ手法」に「多目的遺伝的アルゴリズム」の概念を導入することにより，新たなロバスト最適化手法「多目的シックスシグマ手法」を提案した．本手法をテスト問題に適用することにより，本手法は従来法に比べて高効率かつ利便性に優れた特性を有することが示された．

パレート最適性の概念に基づいた新しい制約条件取り扱い法の開発（2004-2005）
宇宙往還機設計などの現実的な設計最適化問題は複数の目的に加えて，複数の制約条件を持つことが多い．進化アルゴリズムは多目的最適化問題におけるパレート最適解を効率よく得ることが出来ることから，実用的な最適化問題に適した最適化手法であると考えられている．しかしながら，従来は複数の制約条件を重み付き平均した関数を用いるペナルティ法を使っていたため，複数の厳しい制約条件が課された場合に最適な解を効率よく得ることが難しかった．本研究ではパレート最適性に基づいた制約条件の取り扱い手法を開発した．さらに，二段式宇宙往還機の概念設計や圧縮機ファンの詳細設計に本研究で開発された手法を適用し，優れた解が得られることを示した．

NASA GLENN RESEARCH CENTERでの研究テーマ
これらの研究はDr. Meng-Sing Liouと共同で行いました

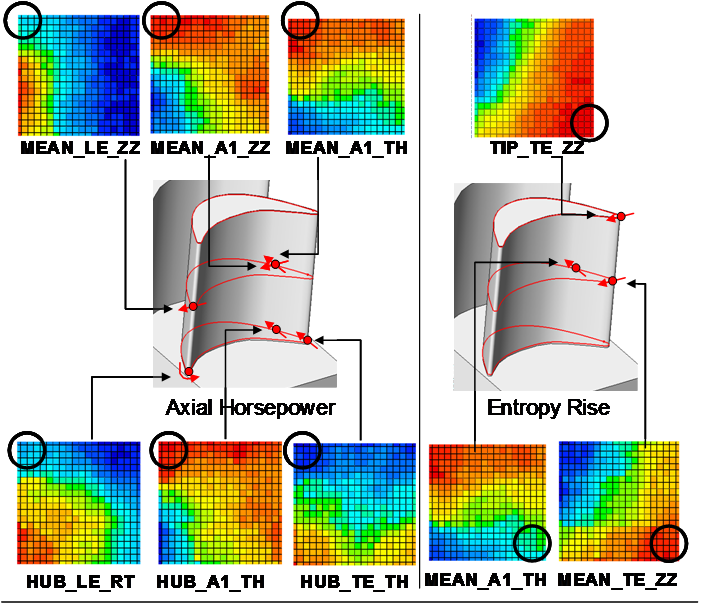
軸流圧縮機動翼の軸流方向及び旋回方向への傾きの最適設計（2002-2003）
航空機エンジン圧縮機の性能向上のための革新的な技術として前進翼列、後退翼列、あるいは旋回方向への傾きを持った翼列の使用が研究されている。ここでは軸流方向及び旋回方向への傾きを持つ軸流圧縮機動翼の最適設計を進化的計算法を用いて行った。従来の動翼形状は翼根から翼端まで一定の後退角を持っていたが、翼端付近で後退角をより大きくとることにより、よりよい空力性能が得られることが示された。

進化的計算法による圧縮機動翼3次元形状の空力設計最適化（2001-2002）
進化的計算法と３次元ナヴィエ･ストークスコードを用いた三次元遷音速圧縮機の翼形状空力最適化手法を開発した。ここで開発された手法は遷音速軸流圧縮機動翼の空力最適化問題に適用され、全圧比や質量流量などの与えられた空力的制約条件を満たしつつ、既存の動翼よりも１９％以上も流れの損失が少ない革新的な動翼形状が得られた。

多段軸流圧縮機の設計最適化手法の開発（2001-2002）
多目的進化的計算法とthrough-flowコードを用いた多段軸流圧縮機の多目的設計最適化手法を開発した。本手法は５段および４段軸流圧縮機の多目的空力設計最適化（効率の最大化および圧力比の最大化）に適用され、ふたつの目的間のトレードオフ解を得ることができた。得られた解のなかには、効率を下げることなく圧力比を９％以上も向上させた解や、与えられた圧力比を保ちつつ効率を１％以上向上させた解が含まれており、本手法の多段軸流圧縮機設計への有効性が示された。

多目的進化的計算法によるターボポンプ概念設計最適化手法の開発（2000-2001）
多目的進化的計算法を用いて、ターボポンプの概念設計最適化ツールを開発した。この手法を単段遠心ポンプの設計と多段ポンプの設計に適用することにより、出力の最大化と必要動力の最小化の多目的設計問題におけるトレードオフの関係が明らかにされた。また、従来のターボポンプより出力及び必要動力の両方において１％以上性能を向上させる設計を得ることができた。